6.1 Areas Between Curves/14: Difference between revisions
Jump to navigation
Jump to search
(Created page with "<math> \begin{align} & y=\cos(x), y=2-\cos(x)\\ & \int_{0}^{2\pi} \left[2 - \cos(x) - \cos(x) \right]\mathrm{d}x = \int_{0}^{2\pi} \left[2 - 2\cos(x)\right]\mathrm{d}x\\ &= \left[ 2x-2\sin(x) \right]\bigg|_{0}^{2\pi}\\ &= \left(4\pi - 0 \right) - \left(0\right)\\ &= 4\pi \end{align} </math>") |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Desmos-graph2.png|300px|left]] | |||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
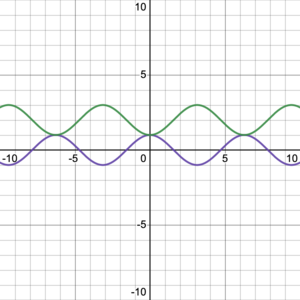
& y=\cos(x), y=2-\cos(x)\\ | & \color{purple}\mathbf{y=\cos(x)}, \color{green}\mathbf{y=2-\cos(x)}\\ | ||
& \int_{0}^{2\pi} \left[2 - \cos(x) - \cos(x) \right]\mathrm{d}x = \int_{0}^{2\pi} \left[2 - 2\cos(x)\right]\mathrm{d}x\\ | & \int_{0}^{2\pi} \left[2 - \cos(x) - \cos(x) \right]\mathrm{d}x = \int_{0}^{2\pi} \left[2 - 2\cos(x)\right]\mathrm{d}x\\ | ||
&= \left[ 2x-2\sin(x) \right]\bigg|_{0}^{2\pi}\\ | &= \left[ 2x-2\sin(x) \right]\bigg|_{0}^{2\pi}\\ | ||
Latest revision as of 19:38, 20 September 2022
![{\displaystyle {\begin{aligned}&\color {purple}\mathbf {y=\cos(x)} ,\color {green}\mathbf {y=2-\cos(x)} \\&\int _{0}^{2\pi }\left[2-\cos(x)-\cos(x)\right]\mathrm {d} x=\int _{0}^{2\pi }\left[2-2\cos(x)\right]\mathrm {d} x\\&=\left[2x-2\sin(x)\right]{\bigg |}_{0}^{2\pi }\\&=\left(4\pi -0\right)-\left(0\right)\\&=4\pi \end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5a4883cde5389d4f0c60fca6be39df1c59efb457)