6.1 Areas Between Curves/18: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary Tag: Manual revert |
||
| (29 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
</math> | </math> | ||
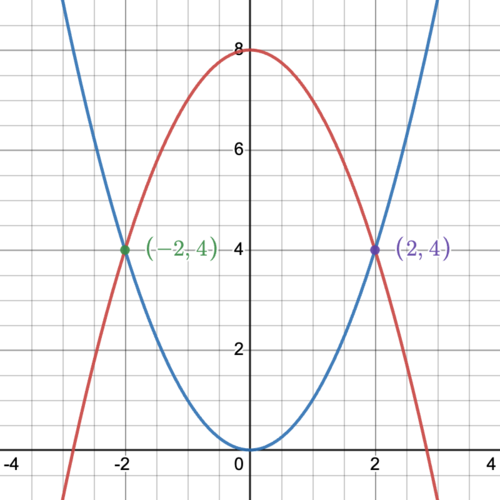
<math>\int_{-3}^{3} \left|(8-x^2) - (x^2)\right|dx </math> | |||
<math> | <math> | ||
| Line 19: | Line 21: | ||
x^2 &= 4 \\ | x^2 &= 4 \\ | ||
x &= \pm2 | x &= \pm2 | ||
\end{align} | |||
</math> | |||
<math>\int_{-3}^{3} \left|(8-x^2) - (x^2)\right|dx = \int_{-3}^{-2}\left((x^2)-(8-x^2)\right)dx + \int_{-2}^{2} \left((8-x^2) - (x^2)\right)dx + \int_{2}^{3}\left((x^2)-(8-x^2)\right)dx = \frac{14}{3} + \frac{64}{3} + \frac{14}{3} = \frac{92}{3}</math> | |||
<math> | |||
\begin{align} | |||
\int_{-3}^{-2}\left((x^2)-(8-x^2)\right)dx &= \int_{-3}^{-2}\left(2x^2-8)\right)dx \\[2ex] | |||
&= \left[\frac{2x^3}{3}-8x\right]\Bigg|_{-3}^{-2} \\[2ex] | |||
&= \left[\frac{2(-2)^3}{3}-8(-2)\right]-\left[\frac{2(-3)^3}{3}-8(-3)\right] \\[2ex] | |||
&= \left[\frac{-16}{3}+16\right]-\left[\frac{-54}{3}+24\right] = \frac{38}{3}-8 \\[2ex] | |||
&= \frac{14}{3} | |||
\end{align} | \end{align} | ||
</math> | </math> | ||
| Line 27: | Line 48: | ||
\int_{-2}^{2} \left((8-x^2) - (x^2)\right)dx &= \int_{-2}^{2}\left(8-2x^2\right)dx \\[2ex] | \int_{-2}^{2} \left((8-x^2) - (x^2)\right)dx &= \int_{-2}^{2}\left(8-2x^2\right)dx \\[2ex] | ||
&= \left | &= \left[8x-\frac{2x^3}{3}\right]\Bigg|_{-2}^{2} \\[2ex] | ||
&= \left | &= \left[8(2)-\frac{2(2)^3}{3}\right] - \left[8(-2)-\frac{2(-2)^3}{3}\right] \\[2ex] | ||
&= \left | &= \left[16-\frac{16}{3}\right]-\left[-16+\frac{16}{3}\right] = 32-\frac{32}{3} \\[2ex] | ||
&= \frac{64}{3} | &= \frac{64}{3} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||




![{\displaystyle {\begin{aligned}\int _{-3}^{-2}\left((x^{2})-(8-x^{2})\right)dx&=\int _{-3}^{-2}\left(2x^{2}-8)\right)dx\\[2ex]&=\left[{\frac {2x^{3}}{3}}-8x\right]{\Bigg |}_{-3}^{-2}\\[2ex]&=\left[{\frac {2(-2)^{3}}{3}}-8(-2)\right]-\left[{\frac {2(-3)^{3}}{3}}-8(-3)\right]\\[2ex]&=\left[{\frac {-16}{3}}+16\right]-\left[{\frac {-54}{3}}+24\right]={\frac {38}{3}}-8\\[2ex]&={\frac {14}{3}}\end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3bdb56d4fb052fa1cca0761b31fb3104c9a31cca)
![{\displaystyle {\begin{aligned}\int _{-2}^{2}\left((8-x^{2})-(x^{2})\right)dx&=\int _{-2}^{2}\left(8-2x^{2}\right)dx\\[2ex]&=\left[8x-{\frac {2x^{3}}{3}}\right]{\Bigg |}_{-2}^{2}\\[2ex]&=\left[8(2)-{\frac {2(2)^{3}}{3}}\right]-\left[8(-2)-{\frac {2(-2)^{3}}{3}}\right]\\[2ex]&=\left[16-{\frac {16}{3}}\right]-\left[-16+{\frac {16}{3}}\right]=32-{\frac {32}{3}}\\[2ex]&={\frac {64}{3}}\end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b34bbaa4ca1bd3009f9c8fd2549e9b85ac66f093)