6.1 Areas Between Curves/23: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (32 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
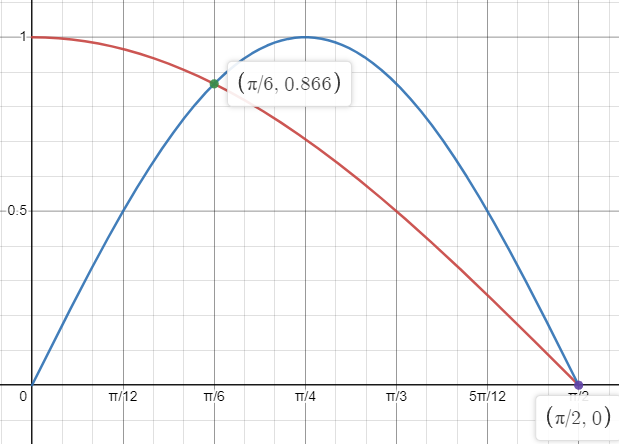
[[File:23.png]] | |||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| Line 22: | Line 24: | ||
<math> | <math> | ||
\int_{0}^{\frac{\pi}{6}} \left(\cos(x) - \sin(2x) \right)dx + \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \left(\sin(2x)- \cos(x) \right)dx | \int_{0}^{\frac{\pi}{6}} \left(\cos(x) - \sin(2x) \right)dx + \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \left(\sin(2x)- \cos(x) \right)dx = \frac{1}{4}+\frac{1}{4} = \frac{2}{4} = \frac{1}{2} | ||
</math> | |||
<math> | |||
\begin{align} | |||
\int_{0}^{\frac{\pi}{6}} \left(\cos(x) - \sin(2x) \right)dx &= \left[\sin(x)+\frac{1}{2}\cos(2x) \right]\Bigg|_{0}^{\frac{\pi}{6}} \\[2ex] | |||
&= \left[\sin(\frac{\pi}{6})+\frac{1}{2}\cos(\frac{2\pi}{6})\right]-\left[\sin(0)+\frac{1}{2}\cos(2(0))\right] \\[2ex] | |||
&= \left[\frac{1}{2}+\frac{1}{2}\left(\frac{1}{2}\right)\right]-\left[0-\frac{1}{2} (1)\right] \\[2ex] | |||
&= \frac{1}{2}+\frac{1}{4}-\frac{1}{2} \\ | |||
&= \frac{1}{4} | |||
\end{align} | |||
</math> | </math> | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
\int_{ | \int_{\frac{\pi}{6}}^{\frac{\pi}{2}} \left[\sin(2x)-\cos(x)\right]dx &= \left[-\frac{1}{2}\cos(2x) - \sin(x) \right]\Bigg|_{\frac{\pi}{6}}^{\frac{\pi}{2}} \\ [2ex] | ||
&= \left[\sin( | &= \left[-\frac{1}{2}\cos(\frac{2\pi}{2})-\sin(\frac{\pi}{2})\right] - \left[-\frac{1}{2}\cos(\frac{2\pi}{6}) - \sin(\frac{\pi}{6})\right] \\[2ex] | ||
&= \left[-\frac{1}{2}\left(-1\right)-1\right]-\left[-\frac{1}{2}\left(\frac{1}{2}\right)-\frac{1}{2}\right]\\ | |||
&= \frac{1}{2}-1+\frac{1}{4}+\frac{1}{2} \\ | |||
&= \frac{1}{4} | |||
\end{align} | \end{align} | ||
</math> | </math> | ||



![{\displaystyle {\begin{aligned}\int _{0}^{\frac {\pi }{6}}\left(\cos(x)-\sin(2x)\right)dx&=\left[\sin(x)+{\frac {1}{2}}\cos(2x)\right]{\Bigg |}_{0}^{\frac {\pi }{6}}\\[2ex]&=\left[\sin({\frac {\pi }{6}})+{\frac {1}{2}}\cos({\frac {2\pi }{6}})\right]-\left[\sin(0)+{\frac {1}{2}}\cos(2(0))\right]\\[2ex]&=\left[{\frac {1}{2}}+{\frac {1}{2}}\left({\frac {1}{2}}\right)\right]-\left[0-{\frac {1}{2}}(1)\right]\\[2ex]&={\frac {1}{2}}+{\frac {1}{4}}-{\frac {1}{2}}\\&={\frac {1}{4}}\end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/97b5c8bf5fdf8b752d48d8a67086e5ec8f6b7629)
![{\displaystyle {\begin{aligned}\int _{\frac {\pi }{6}}^{\frac {\pi }{2}}\left[\sin(2x)-\cos(x)\right]dx&=\left[-{\frac {1}{2}}\cos(2x)-\sin(x)\right]{\Bigg |}_{\frac {\pi }{6}}^{\frac {\pi }{2}}\\[2ex]&=\left[-{\frac {1}{2}}\cos({\frac {2\pi }{2}})-\sin({\frac {\pi }{2}})\right]-\left[-{\frac {1}{2}}\cos({\frac {2\pi }{6}})-\sin({\frac {\pi }{6}})\right]\\[2ex]&=\left[-{\frac {1}{2}}\left(-1\right)-1\right]-\left[-{\frac {1}{2}}\left({\frac {1}{2}}\right)-{\frac {1}{2}}\right]\\&={\frac {1}{2}}-1+{\frac {1}{4}}+{\frac {1}{2}}\\&={\frac {1}{4}}\end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/27b9de09cf7cbbc331aa1e674f662c733bd33c68)