6.1 Areas Between Curves/21: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
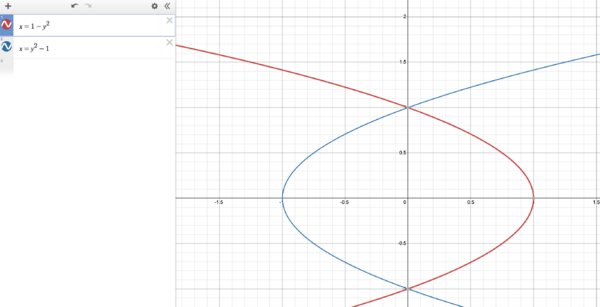
[[File:6.1number21.png|right|600px|]] | [[File:6.1number21.png|right|600px|]] | ||
<math> | |||
\begin{align} | |||
x&=1-y^2, x=y^2-1 \\[1ex] | |||
A &= \int_{a}^{b}[x_R-x_L]dy=\int_{1}^{-1}[(1-y^2)-(y^2-1)]dy\\[2ex] | |||
&=\int_{1}^{-1}[2-2y^2]dy=[2y-2(\frac{y^3}{3})|_{-1}^{0}\\[2ex] | |||
&=2(1)-2(\frac{(1)^3}{3})-[2(-1)-2(\frac{(-1)^3}{3})]\\[2ex] | |||
&=2-\frac{2}{3}+2-\frac{2}{3}=4-\frac{4}{3}\\[2ex] | |||
&=\frac{8}{3} | |||
\end{align} | |||
<\math> | |||
Revision as of 19:49, 22 September 2022
<math> \begin{align} x&=1-y^2, x=y^2-1 \\[1ex] A &= \int_{a}^{b}[x_R-x_L]dy=\int_{1}^{-1}[(1-y^2)-(y^2-1)]dy\\[2ex] &=\int_{1}^{-1}[2-2y^2]dy=[2y-2(\frac{y^3}{3})|_{-1}^{0}\\[2ex] &=2(1)-2(\frac{(1)^3}{3})-[2(-1)-2(\frac{(-1)^3}{3})]\\[2ex] &=2-\frac{2}{3}+2-\frac{2}{3}=4-\frac{4}{3}\\[2ex] &=\frac{8}{3} \end{align} <\math>