6.1 Areas Between Curves/18: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 29: | Line 29: | ||
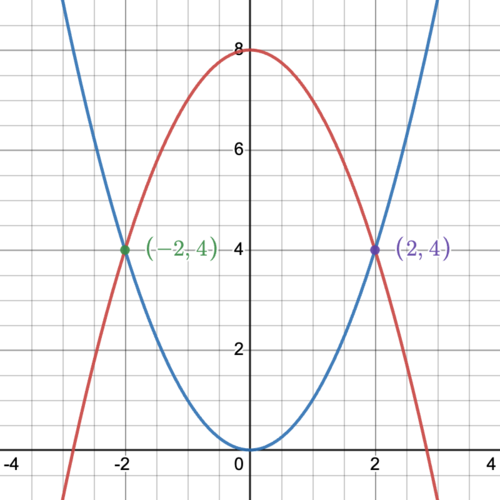
<math>\int_{-3}^{3} \left|(8-x^2) - (x^2)\right|dx = \int_{-3}^{-2}\left((x^2)-(8-x^2)\right)dx + \int_{-2}^{2} \left((8-x^2) - (x^2)\right)dx + \int_{2}^{3}\left((x^2)-(8-x^2)\right)dx</math> | <math>\int_{-3}^{3} \left|(8-x^2) - (x^2)\right|dx = \int_{-3}^{-2}\left((x^2)-(8-x^2)\right)dx + \int_{-2}^{2} \left((8-x^2) - (x^2)\right)dx + \int_{2}^{3}\left((x^2)-(8-x^2)\right)dx</math> | ||
<math> | |||
\begin{align} | |||
\int_{-3}^{-2}\left((x^2)-(8-x^2)\right)dx | |||
\end{align} | |||
<\math> | |||
<math> | <math> | ||
Revision as of 18:02, 13 September 2022
(not done)
Failed to parse (unknown function "\math"): {\displaystyle \begin{align} \int_{-3}^{-2}\left((x^2)-(8-x^2)\right)dx \end{align} <\math> <math> \begin{align} \int_{-2}^{2} \left((8-x^2) - (x^2)\right)dx &= \int_{-2}^{2}\left(8-2x^2\right)dx \\[2ex] &= \left(8x-\frac{2x^3}{3}\right)\bigg|_{-2}^{2} \\[2ex] &= \left(8(2)-\frac{2(2)^3}{3}\right) - \left(8(-2)-\frac{2(-2)^3}{3}\right) \\[2ex] &= \left(16-\frac{16}{3}\right)-\left(-16+\frac{16}{3}\right) = 32-\frac{32}{3} = \frac{96}{3}-\frac{32}{3} \\[2ex] &= \frac{64}{3} \end{align} }