6.1 Areas Between Curves/15: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
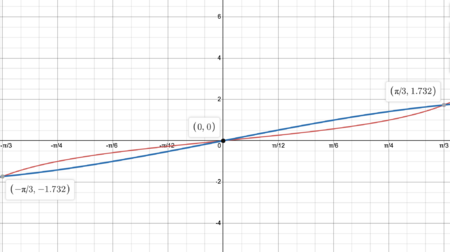
[[File:Screen Shot 2022-09-28 at 4.31.18 PM.png|right|450px|]] | |||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| Line 21: | Line 23: | ||
</math> | </math> | ||
<math>\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}} \left[(\tan(x)) - (2\sin(x))\right]dx = \int_{-\frac{\pi}{3}}^{0}\left[(\tan(x)) - (2\sin(x))\right]dx + \int_{0}^{\frac{\pi}{3}} \left[(2\sin(x)) - (\tan(x))\right]dx = - | <math>\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}} \left[(\tan(x)) - (2\sin(x))\right]dx = \int_{-\frac{\pi}{3}}^{0}\left[(\tan(x)) - (2\sin(x))\right]dx + \int_{0}^{\frac{\pi}{3}} \left[(2\sin(x)) - (\tan(x))\right]dx = 2-\ln(2)-1-1-\ln(2)+2 = -2\ln(2)-2+4 = -2\ln(2)+2</math> | ||
| Line 32: | Line 34: | ||
&= \left[\ln|\sec(0)|+2\cos(0)\right]-\left[\ln|\sec(-\frac{\pi}{3})+2\cos(-\frac{\pi}{3})|\right] \\[2ex] | &= \left[\ln|\sec(0)|+2\cos(0)\right]-\left[\ln|\sec(-\frac{\pi}{3})+2\cos(-\frac{\pi}{3})|\right] \\[2ex] | ||
&= \left[0+2\right]-\left[\ln(2)-2(\frac{1}{2})\right] = - | &= \left[0+2\right]-\left[\ln(2)-2(\frac{1}{2})\right] = 2-\ln(2)-1 \\[2ex] | ||
&= - | &= 2-\ln(2)-1 | ||
\end{align} | \end{align} | ||

![{\displaystyle \int _{-{\frac {\pi }{3}}}^{\frac {\pi }{3}}\left[(\tan(x))-(2\sin(x))\right]dx}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c9f33fdeefca5139a9c6bf920066bc1c44613516)

![{\displaystyle \int _{-{\frac {\pi }{3}}}^{\frac {\pi }{3}}\left[(\tan(x))-(2\sin(x))\right]dx=\int _{-{\frac {\pi }{3}}}^{0}\left[(\tan(x))-(2\sin(x))\right]dx+\int _{0}^{\frac {\pi }{3}}\left[(2\sin(x))-(\tan(x))\right]dx=2-\ln(2)-1-1-\ln(2)+2=-2\ln(2)-2+4=-2\ln(2)+2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/75ad14959fd2617a95b769f206d21262107d1116)
![{\displaystyle {\begin{aligned}\int _{-{\frac {\pi }{3}}}^{0}\left[(\tan(x))-(2\sin(x))\right]dx\\[2ex]&=\left[\ln |\sec(x)|+2\cos(x)\right]{\Bigg |}_{-{\frac {\pi }{3}}}^{0}\\[2ex]&=\left[\ln |\sec(0)|+2\cos(0)\right]-\left[\ln |\sec(-{\frac {\pi }{3}})+2\cos(-{\frac {\pi }{3}})|\right]\\[2ex]&=\left[0+2\right]-\left[\ln(2)-2({\frac {1}{2}})\right]=2-\ln(2)-1\\[2ex]&=2-\ln(2)-1\end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/69bf9719295c930e76f7ab641e003c5313eb4188)
![{\displaystyle {\begin{aligned}\int _{0}^{\frac {\pi }{3}}\left[(2\sin(x))-(\tan(x))\right]dx\\[2ex]&=\left[-2\cos(x)-\ln |\sec(x)|\right]{\Bigg |}_{0}^{\frac {\pi }{3}}\\[2ex]&=\left[-2\cos({\frac {\pi }{3}})-\ln |\sec({\frac {\pi }{3}})|\right]+\left[2\cos(0)+\ln |\sec(0)|\right]\\[2ex]&=\left[(-2)(1/2)-\ln(2)\right]+\left[2+0\right]=-1-\ln(2)+2\\[2ex]&=-1-\ln(2)+2\end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/21356a36c7ff15e4d15667e97c7d9aa1fe050aca)

![{\displaystyle {\begin{aligned}u&=\cos(x)\\[2ex]du&=-\sin(x)\\[2ex]-du&=\sin(x)dx\end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/21cc44bb06026fd5ae3eb49a098fd90de2c3f717)
